What is computation?
According to Leslie Lamport computation is what computational device (or human - my addition) does. It doesn’t matter if it is “useful” calculation or simple bits flipping. More formal way to define computation is to view it as sequence of state mutations.
There is other wide used way to think of computation: functions. Mathematical function maps some input value to some output value. But mathematical function doesn’t care how you get from input to output, but for computation it is big deal. Otherwise there would be no bubblesort, quicksort or other sort algorithms. Computable mathematical function is expected to have output value e.g. halt, while computation can be infinite, think of clock or OS.
What are models of computation?
Models of computation is way to define primitives (operations, storage, alphabet) to carry out computation to be able to do formal reasoning about computations. Being able to do formal reasoning about computation, for example, helped Turing to prove that halting problem generally unsolvable. Formal verification used to prove strength of cryptographic algorithms.
Generally any algorithm explanation assumes some kind of model of computation even if it doesn’t say this explicitly.
Depending on what you are focusing on you may need different model. Knuth described processor with supported instructions to be as close to real world situation as possible. If you want to describe concurrent data structure you need to specify processor (model of computation) with CAS operation. This is just few examples.
Classification of computation models
There are three types of models used in computer science and engineering: abstract machine model, a programming model and a hardware model. Reference.
Abstract machine model
Abstract machine model can alternatively be called a cost model or a performance model.
Those models used for general algorithm research and complexity research. Focus on number of steps required to perform computations. Example: Turing Machine, Sequential State model.
See also: complexity zoo.
Programming model
The programming model provides the semantic of programming abstraction which serves as a basis for the programming language. A primary goal is to allow reasoning about program meaning and correctness.
Interesting fact that some of those models are behind subject, for example OOP. OOP first appeared in 1967 in Simula and was highly developed in 1980-s by Alan Kay in SmallTalk. Design Patterns: Elements of Reusable Object-Oriented Software by GoF appeared in 1994 and Patterns of Enterprise Application Architecture in 2003. But formal models were developed later, for example Formal Methods applied to Object-Oriented Programming in 1992 or Relationships for object-oriented programming languages in 2007 or NOOP A Mathematical Model Of Object-Oriented Programming in 2011 or An Algebraic Formalization of the GoF Design Patterns in 2010 or A Formal Specification of GoF Design Patterns in 1999.
In 1930s Alonzo Church started to work on lambda-calculus.
In 1934 Curry noticed that types of the combinators could be seen as axiom-schemes for intuitionistic implicational logic. It was start for later work on Curry–Howard correspondence or isomorphism which opened up doors to use programs as proofs.
Other notable event here is Chomsky Hierarchy developed in 1956. The classifications are:
| grammar | language | automaton | |
|---|---|---|---|
| type 0 | unrestricted | recursively enumerable | Turing machine |
| type 1 | context-sensitive | context-sensitive | linear-bounded automaton |
| type 2 | context-free | context-free | pushdown automaton |
| type 3 | regular | regular | finite-state automaton |
- The classes are nested, with type 0 being the largest and most general, and type 3 being the smallest and most restricted.
Later Martin Löf extend type theory, which can be applied to programming languages.
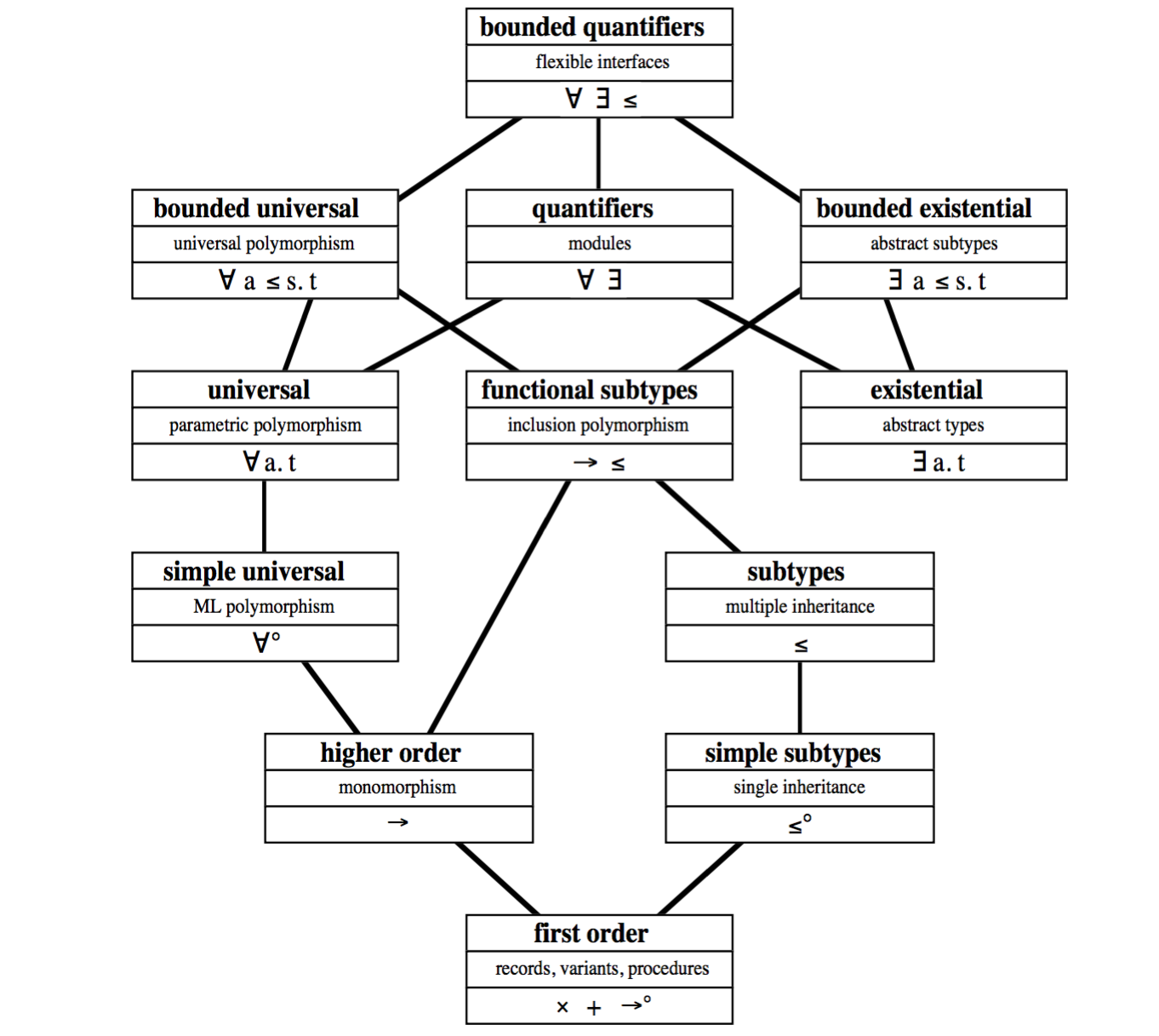
See also: On Understanding Types, Data Abstraction, and Polymorphism
Hardware model
Architectural or hardware model is used for specific language implementation and most notably for the high performance machine (and algorithms optimized for those machine) design purpose.
Example: Von Neumann architecture, pointer machine which used in 6.851: Advanced Data Structures course, MIX (later MMIX) processor used in TAOCP.
What are known models of computation out there?
The most well known is Turing Machine (TM). Introduced by Alan Turing in 1936 in ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM. Most of the time when somebody mentions Turing Machine, they have in mind Universal Turing Machine (UTM) introduced in 1936 paper.
| Author | Year | Papers |
|---|---|---|
| Church | 1936 | Lambda calculus |
| Turing | 1936-7 | Turing Machine (A-machine or Automatic machine) — generic tape-based abstract machine computational. ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM |
| Emil Post | ?1936 | Post-Turing machine — minimalist one-tape, two-direction, 1 symbol (blank, mark) Turing-like machine but with default sequential instruction execution in a manner similar to the basic 3-instruction counter machines. Post Machine, Post Machine Uspensky |
| Goldstine & von Neumann | 1947 | 28 June 1946, 1 April 1947, ECP, The von Neumann Model, The von Neumann Machine |
| Kleene | 1952 | |
| *Hans Hermes | 1954 | |
| Hao Wang | 1957 | Wang B-machine - with only 4 sequential instructions it is very similar to, but even simpler than, the 7 sequential instructions of the Post–Turing machine. W-machine is simply the B-machine with the one additional instruction. —Universal Turing machines: An exercise in coding, —A Variant to Turing’s Theory of Computing Machines |
| *Rózsa Péter | 1958 | |
| Davis | 1958 | Computability & Unsolvability |
| *Ershov | 1959 | |
| *Heinz Kaphengst | 1959 | —Eine Abstrakte Programmgesteuerte Rechenmaschine |
| Zdzislaw Alexander Melzak | 1961 | On a problem in geometrical probability |
| Joachim Lambek | 1961 | HOW TO PROGRAM AN INFINITE ABACUS |
| Marvin Minsky | 1961 | Steps Toward Artificial Intelligence, RECURSIVE UNSOLVABILITY OF POST’S PROBLEM OF “TAG” AND OTHER TOPICS IN THEORY OF TURING MACHINES |
| Shepherdson & Sturgis | 1963 | —Computability of Recursive Functions |
| Elgot & Robinson | 1964 | RASP, —Random-Access Stored-Program Machines, an Approach to Programming Languages |
| Davis | 1965 | Undecidable |
| van Heijenoort | 1967 | |
| Minsky | 1967 | Computation: Finite and Infinite Machines |
| Knuth | 1968–2011 | The Art of Computer Programming, MMIX |
| Hartmanis | 1971 | —Computational complexity of random access stored program machines |
| Cook & Reckhow | 1972 | Time Bounded Random Access Machines |
| Carl Hewitt | 1973 | Actor model |
| Kahn | 1974 | Kahn Process Network |
| Hoare | 1978 | Communicating Sequential Processes, Process Calculi |
| Arnold Schönhage | 1979 | —Storage Modification Machines |
| Milner | 1980 | Calculus of Communicating Systems, Process Calculi |
| Lee | 1986 | Synchronous Dataflow |
| van Emde Boas | 1989 | Machine models and simulations |
| Boolos & Burgess; Boolos, Burgess & Jeffrey | Computability and Logic |
TODO: implement Narrative Chart for models of computation.
Turing machines
Basically Turing machine - is a tape machine capable to do some set of operations like write, erase, move left or right. Number of operations may differ, number of tapes may differ too. Tape is infinite.
By Turing:
- Automatic (A) machines motion completely determined by the configuration.
- Choice (C) machine, whose motion is only partially determined by the configuration.
- Oracle (O) machines is a A-machine that pauses its computation at some state, to complete its calculation, it awaits the decision of the oracle — an unspecified entity.
- Universal (U) machine. It is possible to invent a single machine which can be used to compute any computable sequence. If this machine U is supplied with the tape on the beginning of which is written the string of quintuples separated by semicolons of some computing machine M, then U will compute the same sequence as M.
By Wang:
- B-machine - with only 4 sequential instructions it is very similar to, but even simpler than, the 7 sequential instructions of the Post–Turing machine.
- W-machine is simply the B-machine with the one additional instruction.
Other:
- Non-deterministic (NTM) Turing machine. Differs from deterministic machine by the fact that current state can have more than one next states. Note: it implements bounded non-determinism.
- Probabilistic (PTM) Turing machine is a non-deterministic Turing machine which chooses between the available transitions at each point according to some probability distribution.
- Neural Turing Machines which are gone pretty far from original one tape machine.
See also:
- Turing’s Ideas and Models of Computation
- The Origins of the Turing Thesis Myth
- Turing’s Influence on Programming
Survey of the sequential and parallel models of computation
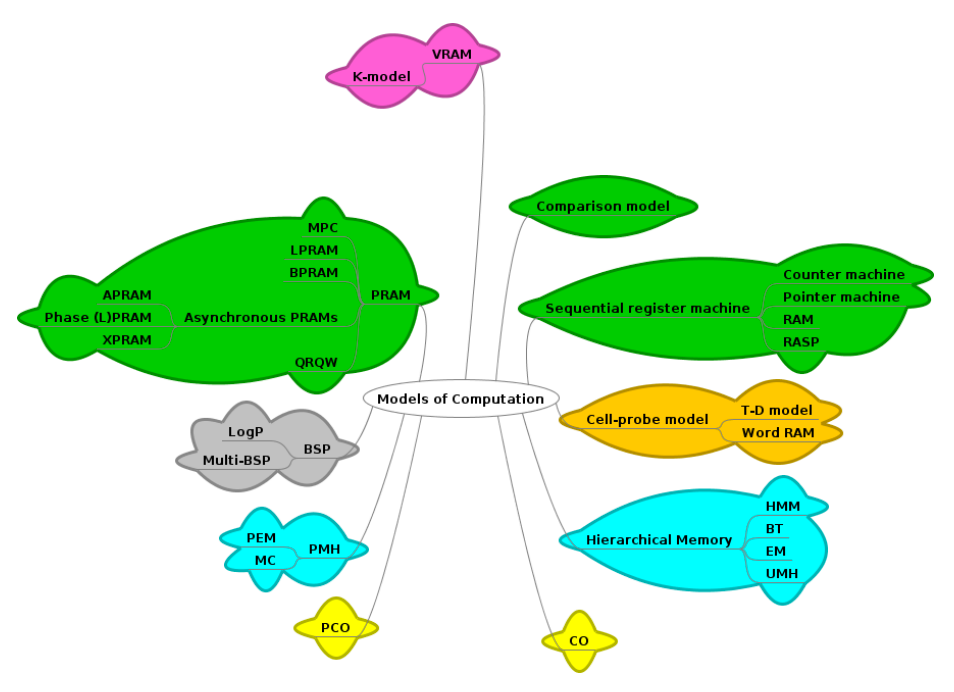
Other Notes
There is also Actor System, which claims to be able to implement unbounded non-determinism, according to Carl Hewitt. While TM only able to implement bounded non-determinism.
Unproved claim: bounded nondteremenism corresponds to system where next step is non-determined, unbounded non-determinism corresponds to the system where order of steps non-determined.
Some authors claims that output device would make difference for TM. I believe Turing meant tape to be used as memory and output device. When he build working prototype of computer he used Williams tubes as memory and as output device.